Inverse Optimal Control
What is Inverse Optimal Control (IOC)
In nature, many behaviours can be modelled as optimal control, for instance:
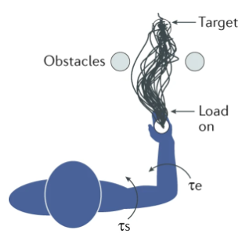


On the other hand, optimal control are widely used in many applications, for instance:
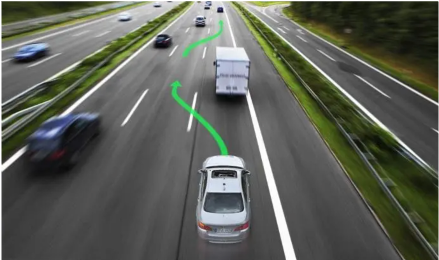
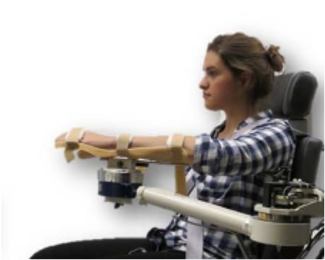
The fundamental problem of optimal control is to design the objective function so that the corresponding agent behavior is adapted to suit the contextual environment. In addition, if we are interested in modelling the expert’s (bee, stock manager, etc.,) decision process, we would like to estimate her decision criterion.
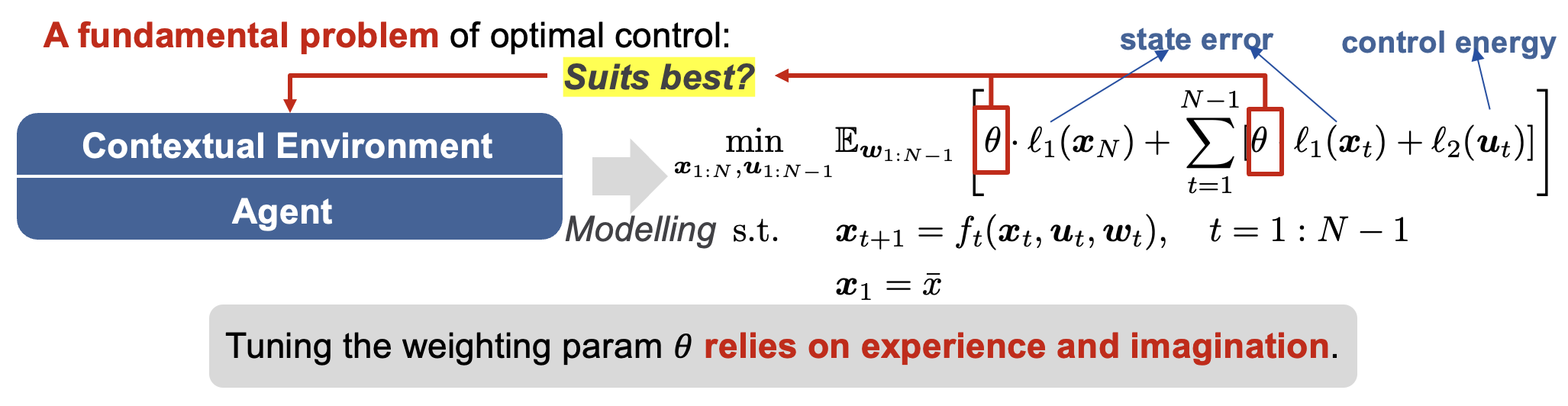
The goal of IOC: identify the unknown param from the observed expert data. This makes IOC a perfect tool for identifying the decision process model for expert systems. Moreover, IOC provide a powerful tool for tuning the parameters of optimal control problems (Model Predictive Control, etc.). One only need to “learn” the parameter that suits the contextual environment from the expert system’s demonstration.
Category of the IOC problem
The optimality conditions of the underlying optimal control problem actually defines a model structure. Hence such problem is categorized as a grey-box system identification problem.
Challenges
-
Stochasticity is involved in the entire process. In particular, there are randomness when an agent makes her decision. In addition, for a given task, the time instant for a agent to start performing the control, or in other words – make decisions, is also random. It is essential to design a system identification algorithm that is robust to these randomness.
-
System identification algorithm is usually based on solving an optimization problem. Local minima is usually inevitable and impairs the accuracy of the estimation.
-
IOC problem are usually ill-posed. There might be multiple objective function that corresponds to the same control input. Namely, identifiability can not be guaranteed.
Our work
We have done quite a few work on this topic. See ‘Publications’ for more details.