Modeling human's tracking behaviour
Identifying human's decision criterion based on Inverse Optimal Control
(See “Han Zhang, Axel Ringh, Weihan Jiang, Shaoyuan Li, Xiaoming Hu. Statistically Consistent Inverse Optimal Control for Linear-Quadratic Tracking with Random Time Horizon, Proceedings of the 41st Chinese Control Conference (CCC)” for more details.)
In this project, we try to model how human tracks a given reference signal in rehabilitation trainings. In particular, the patient is seated at a desk in front of a screen. On the desk there is a crank, with viscosity (damping), which when rotated moves a pointer left-andright on the screen. The patient is repeatedly asked rotate the crank to track a pointer whose movement is governed by a given reference signal.
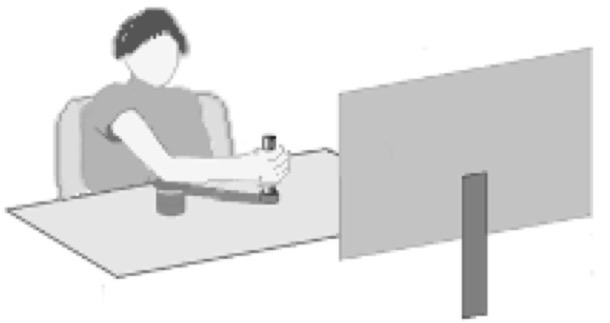

There are basically several challenges to model such human’s tracking behaviour:
-
Stochasticity is involved in the entire process. In particular, there are randomness when a human makes her decision. In addition, given a reference signal, the time instant for a human to start tracking is also random. It is essential to design a system identification algorithm that is robust to these random noises.
-
System identification algorithm is usually based on solving an optimization problem. Local minima is usually inevitable and impairs the accuracy of the estimation.
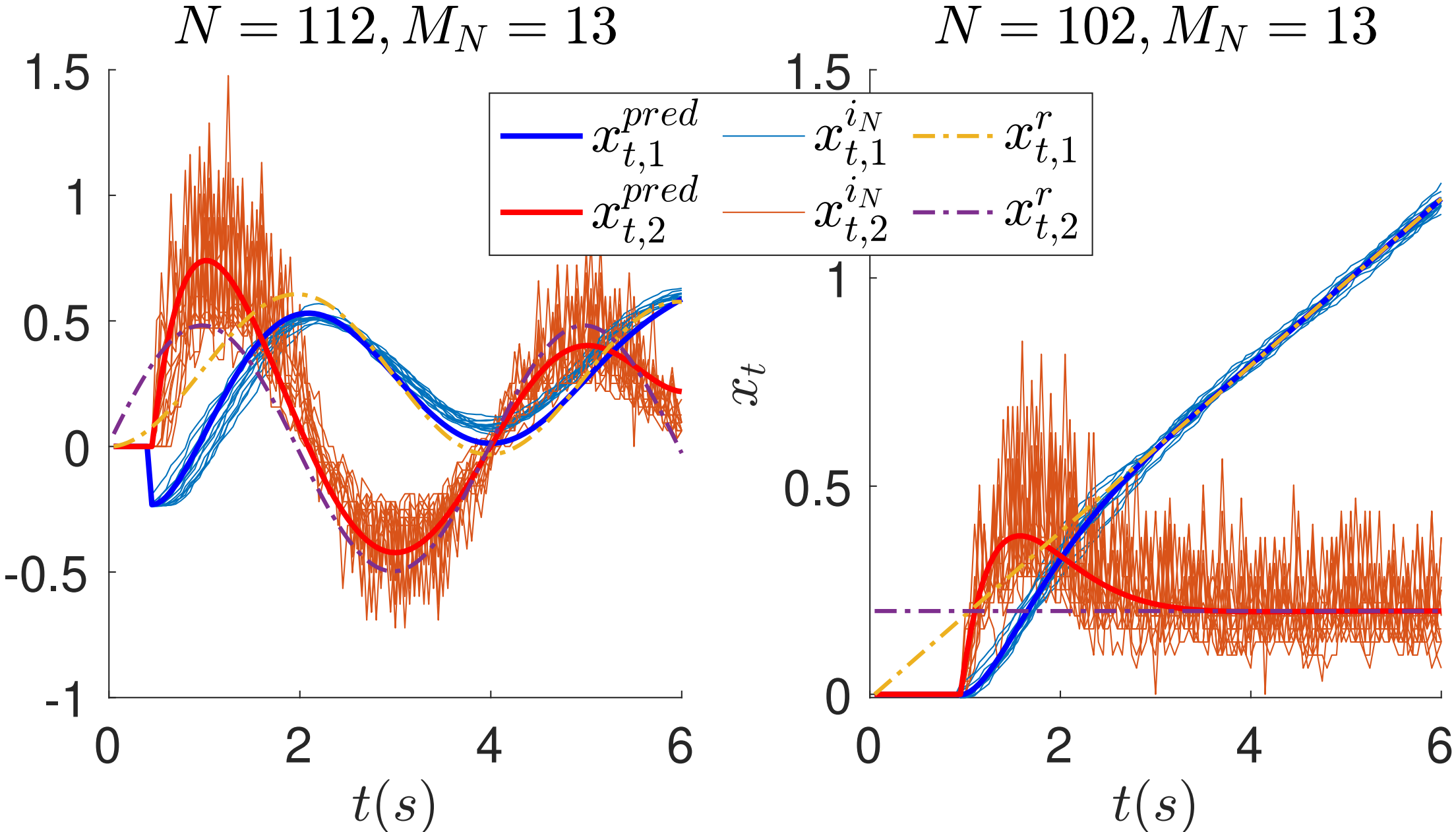
To this end, we model the tracking behaviour of human in such rehabilitation training as a linear quadratic optimal tracking problem with random time-horion length. We have managed to design a statistically consistent estimator that is based on convex optimization. This means that we can mitigate the trouble caused by noise by adding more data. The estimate result would converge to the “true” value as the data amount grows. Moreover, since the estimator is based on a convex optimization problem, it does not suffer from local minima issues.
To validate the precision of the model, we let the human to track reference signals that are different from the one that is used for system identification. It shows that we obtain a quite accurate prediction.